Analyzing the Fine Structure of Mercury Through the Zeeman Effect
Over the summer of 2014 I was enrolled in SSC-479R at The University of Texas at Austin as part of completing the Certificate in Scientific Computation. Below is the executive summary and a link to the entire research paper. The research was conducted with Dr Greg O. Sitz acting as the research advisor. Many thanks go to him for all his great advice.
Executive Summary
Quantum mechanical processes are often difficult to observe due to their intrinsic small scale. However, the observation of these processes can yield benefits in macro scale applications such as carbon dating, communications, spectroscopy, and others. One such quantum mechanical processes is the Zeeman Effect. The Zeeman Effect provides a method to observe the change in quantum mechanical energy levels due to the presence of an external magnetic field. With the advent of high resolution interferometry, a classical spectrometer is no longer needed to perform this observation.
Spectral interferometry recorded by digital photography provides a method to analyze the visual data in an automated manner. The analysis of spatially resolved imaging using a scripting language such as python provides the automated method. We examine the Zeeman Effect of Hg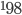 discharge lamp within a magnetic field range of .47 ±.008 Tesla to .83 ±.008 Tesla. With the use of python, fluctuations in the intensities of the rings visible through an interferometer can be averaged out and provide a greater confidence in the observed values.
discharge lamp within a magnetic field range of .47 ±.008 Tesla to .83 ±.008 Tesla. With the use of python, fluctuations in the intensities of the rings visible through an interferometer can be averaged out and provide a greater confidence in the observed values.
The examination of the behavior of the 6s7s 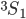
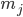 =-1 to 6s6p
=-1 to 6s6p 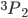
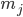 =-1 spin state transition of a Hg
=-1 spin state transition of a Hg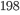 discharge lamp in the magnetic field, produced a linear relation for the change in spatial frequency and magnetic field of -23.74
discharge lamp in the magnetic field, produced a linear relation for the change in spatial frequency and magnetic field of -23.74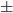 4.17 mm
4.17 mm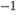 T
T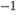 with an intercept of .83
with an intercept of .83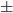 2.76 mm
2.76 mm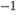 . Similarly, a linear relationship of 28.11
. Similarly, a linear relationship of 28.11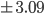 mm
mm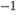 T
T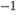 with an intercept of -4.50
with an intercept of -4.50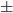 2.05 mm
2.05 mm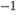 was found for the 6s7s
was found for the 6s7s 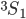
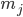 =1 to 6s6p
=1 to 6s6p 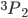
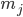 =1 spin state transition. The linear values differ from the accepted values by +2% and +20% respectively. The accepted values are -23.33 mm
=1 spin state transition. The linear values differ from the accepted values by +2% and +20% respectively. The accepted values are -23.33 mm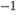 T
T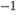 for the
for the 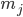 =-1 transition and 23.33 mm
=-1 transition and 23.33 mm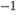 T
T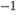 for the
for the 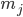 =1 transition. Using the implemented method to analyze the
=1 transition. Using the implemented method to analyze the 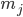 =-1 state transitions provides a moderately agreeable result, however, in future investigations, a different method must be employed to calculate the
=-1 state transitions provides a moderately agreeable result, however, in future investigations, a different method must be employed to calculate the 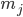 =1 state transitions that account for the susceptibility of the method to off axis intensity peak skewing.
=1 state transitions that account for the susceptibility of the method to off axis intensity peak skewing.
Link to full research paper covering the Zeeman Effect.
0 Comments on “Analyzing the Fine Structure of Mercury Through the Zeeman Effect”